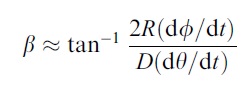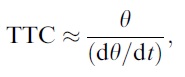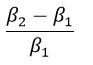[shadowbox]
Pitch Tunneling & Perceptually Equivalent Pitches
Recently I have become fascinated with the topic of pitch tunneling, not only because I am a big baseball fan but because it bears a striking resemble to some of the psychophysical experiments I did during my PhD (and since). Specifically, one’s designed to measure discrimination thresholds for the direction of motion in depth and the time to contact of an approaching object. There are also a few ways that I think the idea of pitch tunneling can be improved and expanded upon. Let me explain…
Visual Information about “Where” and “When”
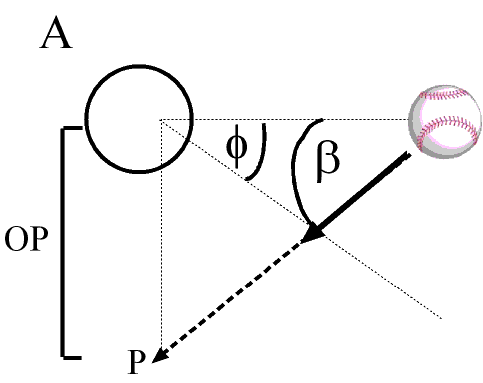
When a ball is pitched there are key sources of visual information that can be used to judge its trajectory. Remember human beings don’t have radar guns or pitch f/x cameras built into their heads so we don’t see our visual world in terms of mph, feet and rpm….we see it in terms of visual angles. For determining where a pitch is headed vertically (e.g., whether it will cross at the knees or belt) there are two angles that are relevant, as illustrated in the figure below where the big circle is the batter’s eye:
Figure 1
The first angle (Φ) specifies the visual direction of the ball relative to our body axis..this can be picked up directly. The second angle (β) specifies the angular direction of motion in depth relative to the launch point of the pitch. Because it is not defined relative to our eye we don’t have direct access to it and instead have to do a little work to get it. Specifically,
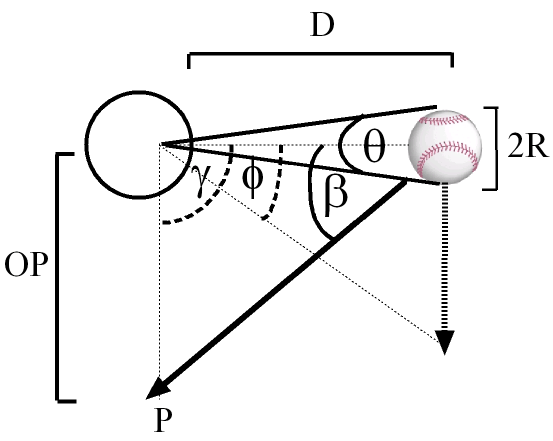
where R is ball’s radius, D is it’s distance from the eye, dΦ/dt is the rate of change of its visual direction and rate dθ/dt and the rate at which the angular size of the ball (θ) is expanding, as shown in the figure below:
Figure 2
Note, here I am only considering vertical direction – I will tackle horizontal direction in a future post.
The other important thing we need to know is the time at which the ball arrive at the plate, referred as the time to contact (TTC). This is specified by the following optical information:
Perceptual Thresholds for “Where” and “When”
OK, back to the experiments I mentioned. Imagine that we throw two pitches in a row at a batter, one with angular direction β1 and one with angular direction β2 as shown in the figure below:
Figure 3
How well will the batter be able to tell them apart? In the terminology of psychophysics, what we are trying to determine here is the discrimination threshold for the direction of motion in depth — or stated another way, the smallest difference between β1 and β2 the hitter will be able to reliably detect in order to tell they are different pitches. In our experiments, we repeatedly present the observer with pairs of pitches (lets call them pitch 1 and pitch 2)…if you are familiar with concept of tunneling this should be starting to ring a bell now. In the experiment, pitch 1 always has the same value of β, while the β value for pitch 2 changes from pitch-to-pitch. The observer’s task is to judge whether Pitch 2 is travelling at a lower or higher angle than Pitch 1. As you can imagine, when the β values for the two pitches are very similar this judgment is very difficult. In the experiment, we keep changing the β value for Pitch 2 until we find the smallest difference in β the observer can reliably judge (usually defined as with 75% accuracy)…this is the discrimination threshold.
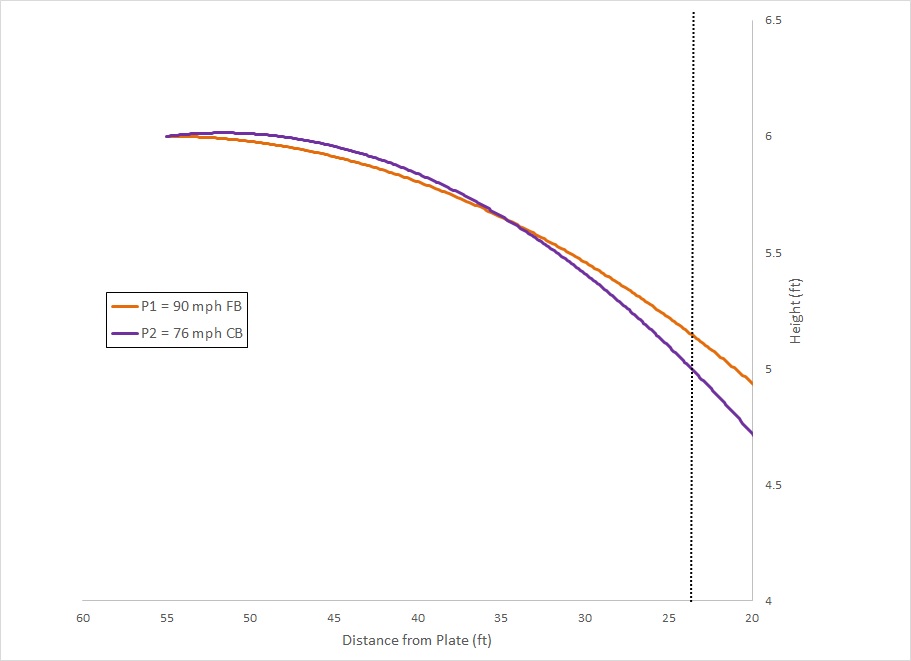
When we express threshold values it is typically done using what is called a Weber fraction – that is, we express them as a proportion of the value of the comparison stimulus (Pitch 1 in my example). This allows us to make more meaningful comparisons. Imagine I asked you to tell me which was heavier: a weight that was 5 lb or a weight that is 10 lb. You could easily do it. But (assuming you can lift them) could you tell the difference between a weight that was 105 lb and one that was 110 lb? Not likely! Even though the difference is the same. Weber fractions capture the fact that the difference between two things needed to tell them apart increases as the value of the comparison stimulus increases (e.g. from 5 lb to 105 lb in my example). So, a discrimination threshold for β would be of the form:
Where the numerator is the smallest difference in angle we can detect and the denominator is the angle pitch 1 was thrown at.
In very well controlled lab experiments where the observer is using a head rest and bite bar (a device that looks likes it something used for a medieval torture..see below!) to help keep their eyes and head still, β discrimination thresholds can be tiny…with Weber fractions ranging from about 0.1 to 0.2.
I have repeated these experiments with experienced baseball players, in their batting stance, that were required to swing the bat after making the judgment, and with the distance and size of the ball simulated accurately. As you can imagine, the story was a bit different. For these experiments, I got values (unpublished) for the β discrimination threshold that ranged from about 0.5-0.8 so that’s what I am going to use in the calculations below. You can also do similar experiments to determine discrimination thresholds for Φ and TTC, but let’s get to pitch tunneling.
Pitch Tunneling
When trying to get a batter out, pitchers typically are concerned with the end of a pitch’s trajectory – where does it cross the plate and does it have “late movement”. The concept of pitch tunneling is the idea that it can also be effective to focus on the early part of the pitch trajectory. Specifically, if two pitches (say a 90 mph fastball and a 76 mph curveball) can travel down the same initial trajectory long enough the batter won’t be able to tell them apart before they need to start their swing — despite the fact the two will end up in very different locations. This is illustrated very nicely in this overlay from Driveline Baseball:
Here’s a perfect 4 seam FB/2 seam FB tunnel overlay by @brandonmmann in ScratchReel form 👍🏻 pic.twitter.com/9qubSDnPki
— Driveline Baseball (@DrivelineBB) January 20, 2017
Obviously hitting a 90 mph fastball and a 76 mph curveball require completely different swing parameters, so if they batter can’t tell which is which before they need to swing they are going to be in a pickle! So, pitches that travel with the same initial trajectory are said to travel down the same “pitch tunnel”. Although I like the more colorful term Greg Maddux used: “column of milk travelling to home plate”.
OK, that’s all well and good but how do we know whether or not two consecutive pitches travel down the same pitch tunnel? Baseball Prospectus has created a series of measures around the concept of pitch tunneling. Their most basic measure is called the “tunnel differential” which is the vertical separation between two pitches (expressed in inches) at the “tunnel point”. The tunnel point is when the ball is 23.8 feet from the plate. This value is chosen because it is assumed the movement time of a swing is roughly 175 ms and an average major-league fastball will reach this value of time before contact at about 23.8 feet. So, 23.8 feet is the “point of no return” for an average fastball and an average MLB hitter. The decision about how to swing must be made before this. (Note, it is possible and more appropriate to define the tunnel point perceptually but for today I will take this 23.8 feet mark as gospel). Just for reference, as I write this, the current league leader in tunnel differential (averaged across all their pitch pairs, minimum 500 pairs) is Jacob DeGrom with a differential of 8.5” while at the bottom of the scale we have Rich Hill with a differential of nearly 1 foot. However, these average values are not likely to be too informative because they will include lots of cases where the pitcher was not deliberately trying to tunnel.
While I recognize this is an initial attempt at quantify pitch tunnels, I have two major issues with the tunnel differential measure. First, a tunnel is a 3D volume not a single point. What if two pitches have very different trajectories leading up to tunnel point but have the same value at it? Imagine throwing a “laser beam” and a looping throw that both hit the same spot when they are 23.8 feet from the plate. The batter would easily be able to tell them apart. Having a decision “point” does not mean a batter can’t use information that occurs before the point. This is also relevant to how pitchers are being taught to “throw in tunnels” which I will discuss shortly. The second issue I have with the tunnel differential is that it is expressed in inches. As I have already tried to emphasize we don’t perceive our world this way so it will be much more meaningful to discuss tunnels in terms of perceptual information…
Perceptual Thresholds & Pitch Tunneling
Let me introduce a new definition of pitch tunneling. Two pitches travel down the same tunnel when the visual information sources used for judging direction and TTC are kept below the batter’s discrimination threshold until they reach the decision point. If a pitcher can achieve this it will result in “perceptually equivalent pitches”, that is pitches that will be perceived as the same by the batter even though they might have vastly different physical parameters.
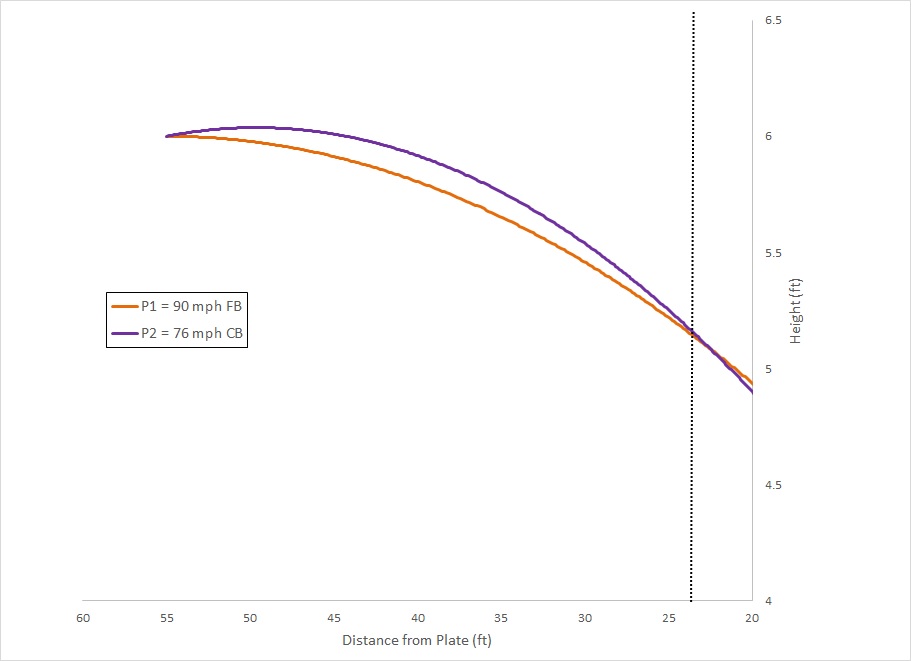
Let me run through a few examples to illustrate. Below I show the trajectories of two pitches – a 90 mph fastball (FB) and a 76 mph curveball (CB). Note, for these, I have assumed vanilla, league average values for movement and spin rate. I will look at the effect these other parameters have on tunnels in future posts. In this example, both the FB and CB would cross the plate at a height of roughly 3.4 feet.
Figure 4
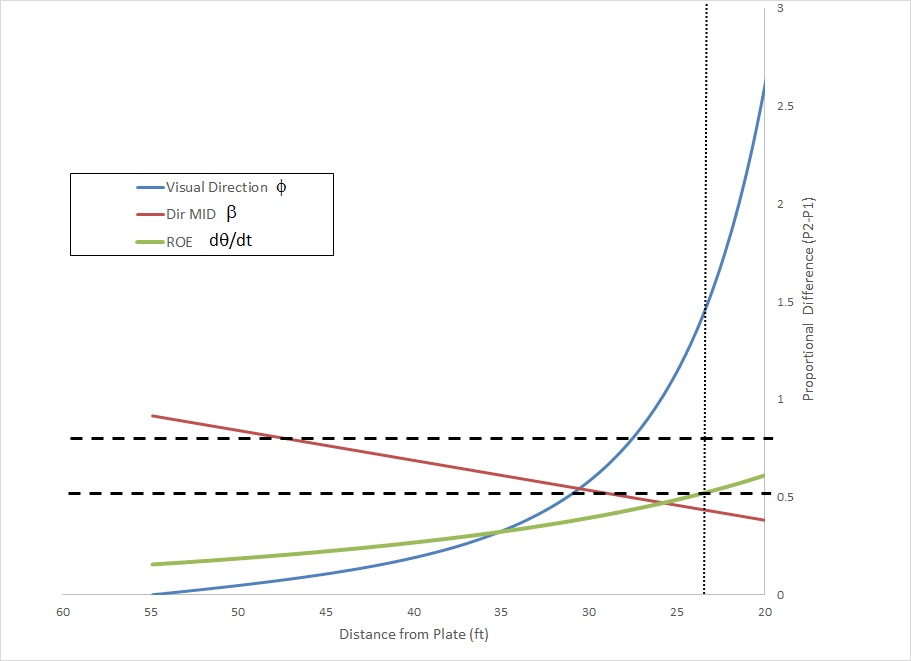
What can be seen here is that when the pitcher wants the same outcome (cross the plate at roughly the same height) the initial trajectories are very different. We see the “hump” in the curveball batter’s are taught to look for. In this figure, the tunnel differential (at the decision point shown by the dotted vertical line) is roughly 6”. So these two pitches should be easy to tell apart. But what does the perceptual information have to say:
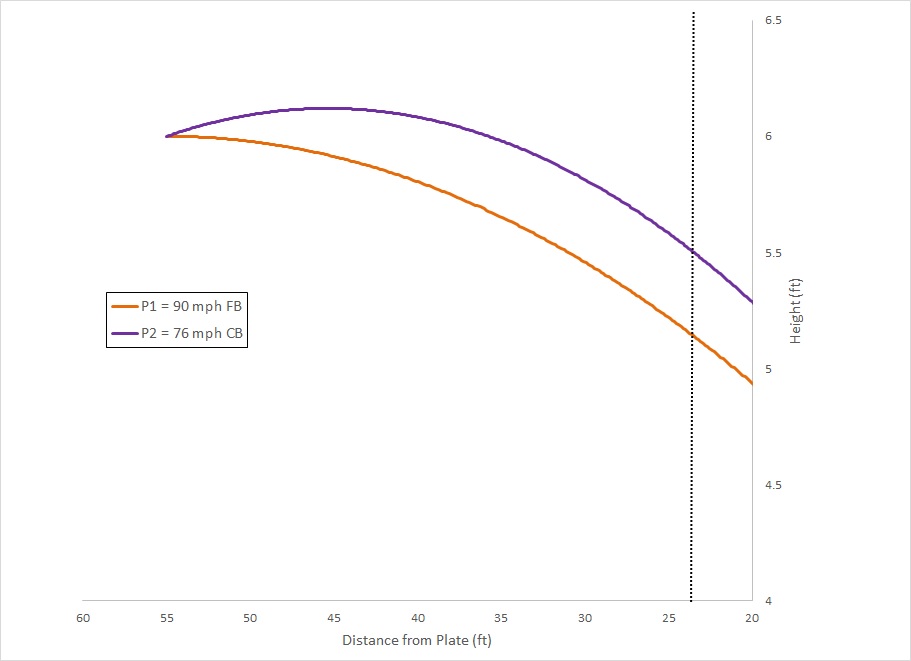
Figure 5
This confirms our intuition. The difference in direction (β) between the two pitches is well above the discrimination threshold range (horizontal dashed lines) from the moment the ball is released all the way up to the decision point. So much so I had to move my legend! The visual direction (Φ) goes above threshold well before the decision point too (at about 35 feet from the plate). So in terms of the direction of travel these pitches are not perceptually equivalent. But what about the other (green) line in the figure? This shows the rate of expansion of the ball’s image (dθ/dt) which is used to judge time to contact. The fact that it stays below threshold up to the decision point provides support for a claim made by Greg Maddux that “no hitter could tell the speed of a pitch with any meaningful accuracy”. Even for a difference in speed between the pitches of 14 mph, the difference in the visual information that is related to speed (dθ/dt) is below threshold up to the decision point so the batter cannot tell the pitches apart based on this variable alone.
Ok, let’s look at a different pair of pitches where the pitcher attempts to achieve a tunnel.
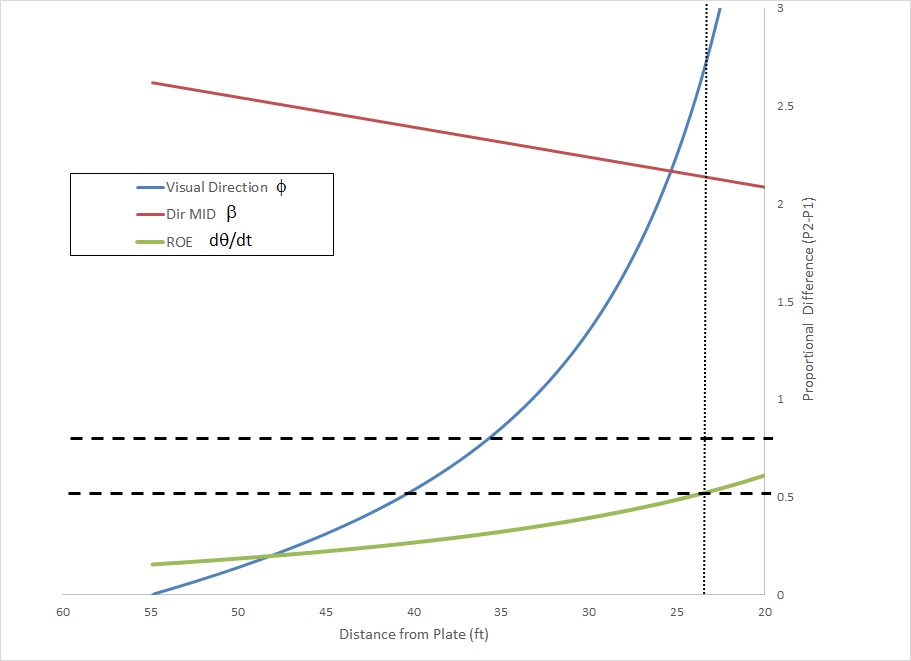
Figure 6
Now we have a tunnel differential at the decision point of only 1.8”. But, of course, this means the outcomes of the two pitches will be different, with the FB crossing the plate at a height of 3.4 feet and the CB at 2.4 feet. Let’s look at the perceptual information:
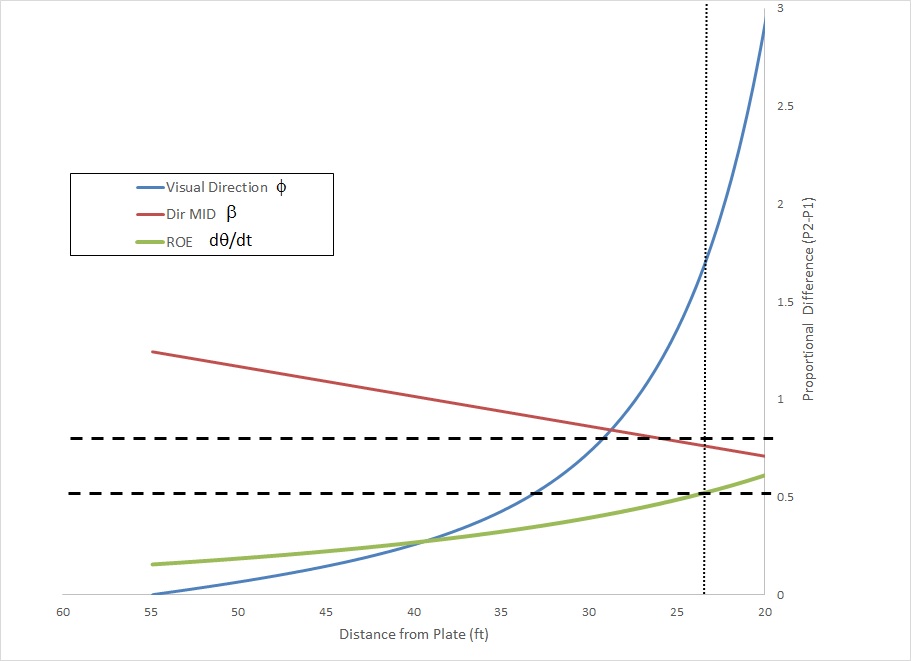
Figure 7
This time the β difference remains right around the threshold range for the entire trajectory and the Φ difference only rises above the range just before the decision point. Therefore, except for batters with really high sensitivity, these pitches ARE perceptually equivalent up to the decision point.
One final example of a point I was trying to make earlier. Here are two pitches that have 0 tunnel differential at the decision point.
Figure 8
But when we look at the perceptual information we see:
Figure 9
While the β difference dips into the threshold range at the decision point, it was above this for much of time before. Unless we assume that batters don’t take in information continuously and instead only use it at one discrete time point (which I think is unlikely), these pitches are not perceptually equivalent! In terms of pitch tunneling, it not only matters where you are at the tunnel point but also how you got there.
A Few More Twists
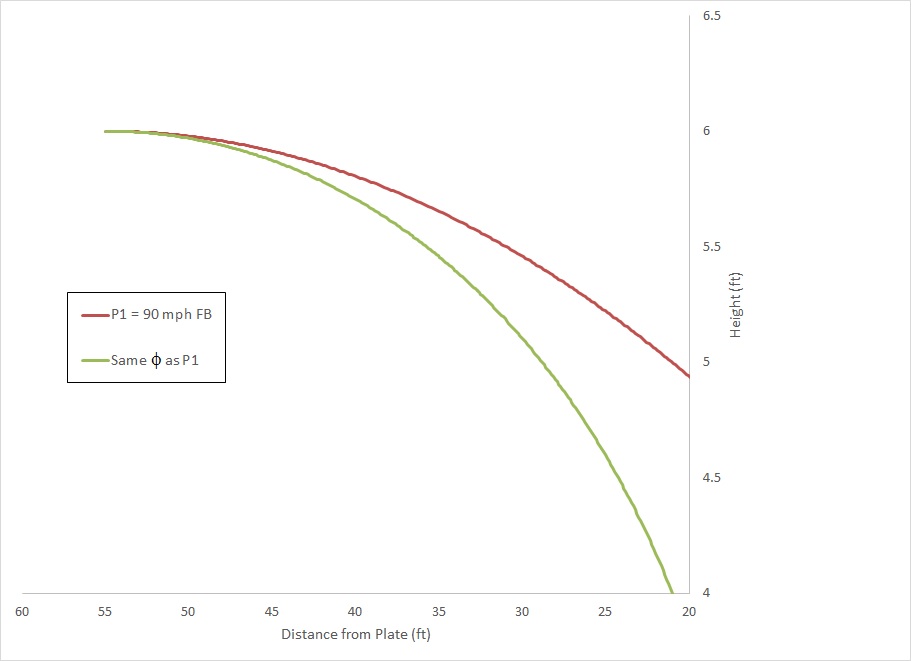
So far I have been focusing on achieving pitch tunneling by keeping the direction of motion in depth (β) difference below threshold during the early part of the ball flight. As can be seen Figure 6 above, this essentially involves having two pitches travel the same path through physical space. But there is another radically different way we could do it by looking at the visual direction Φ. In terms of this source of information, these two pitches are perceptually equivalent:
Figure 10
What?! Yep, the pitch shown by the green line (which would hit the ground a few feet in front of the plate!) has the same visual direction throughout its flight as the 90 mph fastball. Another way to think of this is: if I filmed these two pitches from the batter’s perspective then superimposed the videos, you would only ever see one ball. I am not showing it here, but of course, the β difference would be WAY above threshold! As shown in Figure 3, two pitches can have the same Φ value but have a very different β. But, it has been argued by some that we judge the direction of moving objects based on visual direction. Could it be case that for some instances where batters swing wildly at a pitch in the dirt it has the same visual direction (Φ) as the previous pitch? Hmm…
Returning to my PhD experiments I talked about earlier, I think it might make sense to also extend the idea of pitch tunneling beyond pairs of consecutive pitches. As mentioned, in our experiments (for which I also always served as an experimental participant) we looked at pairs of pitches, P1 that was always the same and P2 that changed from trial to trial. Well after hours of doing this I thought to myself: why don’t I just stop presenting P1. Since it is always the same maybe I could just memorize its trajectory and thus cut the time it takes to complete the experiment in half. Sure enough this was easy to do. In fact, as long as you give a participant feedback about whether their judgment is correct you don’t need to even present P1 once! They can learn what it is (presumably developing an internal model of it) and end up performing just as well as when it is presented on every trail. Could the same be true of batters? When they face the same pitcher a lot do they develop internal models of his most common pitches? If this is true it might be possible for a pitcher to create a “tunnel effect” by making their next pitch perceptually equivalent to their most common pitch rather than the one thrown before.
The last point I will make concerns training. I have heard that coaches are now trying to teach pitchers to tunnel by having them thrown pitches through a hula-hoop placed at the decision point distance of 23.8 feet. Hopefully, as illustrated in Figure 8 above, I have convinced you that this will not necessarily produce perceptually-equivalent pitches. Instead I think what should be done is practice throwing through 2 hoops of different sizes placed at different distances. On the flip slide, we have found that these perceptual thresholds can be improved with practice, therefore, it may be possible for a hitter to defeat tunneling with appropriate training. I will talk about exactly how to do this in future posts 🙂
Take Home Messages
- When we are talking about things related to a batter’s vision like tunneling we need to analyze things in terms of perceptual information not physical variables like feet and mph.
- Pitch tunneling should be defined as throwing consecutive pitches such that the perceptual discrimination thresholds for information about trajectory are below threshold until the decision point is reached.
- When we re-focus it in terms of perceptual information, I think pitch tunneling is an even more interesting concept with lots of potential.
- In future posts, I am going to explore these ideas more including some analysis of MLB pitcher data
Footnotes and References:
- Unconfounding the direction of motion in depth, time to passage and rotation rate of a simulated approaching object
- Technically, the optical variable that is relevant for timing is time to passage (TTP, the time it will take until the ball passes a location some distance from the eye such as P in Figure 1) not time to contact but for the distances were are talking about here they are effectively the same.
- Using visual direction in three-dimensional motion perception
[/shadowbox]