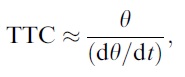[shadowbox]

Why is it difficult to catch a poorly thrown or kicked football? A perceptual perspective

With the NFL preseason underway I thought I would turn my eye to the gridiron. For a football quarterback or punter it is advantageous to throw (or kick) the ball so that it travels in a perfect spiral for a few reasons. First and foremost, as explained in the video below, making the ball spiral (that is adding spin perpendicular to the direction of travel) adds angular momentum to the ball which makes it hold a constant orientation  throughout its flight. Holding a constant orientation means the shape of the ball stays consistent making the air resistance forces acting on it pretty consistent. The net result is a longer and more accurate pass or kick.

But making the ball travel in spiral also has consequences at the other end for receivers and returners. If you have watched a lot of football, you will have probably noticed that kicks or passes that do not travel with a perfect spiral (e.g. an end over end kickoff) are difficult to catch and are often dropped or missed.

In sports like rugby, non-spiral kicks are often done purposely to make receiving the ball more difficult.

So why exactly is it so difficult to catch a poorly thrown or kicked ball? Part of it has to due with knowing where the ball is going to end up. As described in the video above, when a ball does not travel in a spiral the air resistance forces are unpredictable making it harder for the receiver or returner to predict the trajectory.  However, as can be seen in the photos above, muffs and drops also seem to happen when the receiver is perfect aligned with the ball’s travel so this poor prediction of trajectory can’t be the whole story.

Grasping Tau

A key to catching a football is obviously being able to tell when it will arrive at your body so you can close your hands at the right time. For a receiver or punt returner this can be done very easily by  using the rate of expansion of the ball’s image on the eye. Specifically the time until the ball will contact the receiver’s hands (TTC) is given by:

where θ is the angular size of the ball’s image and dθ/dt is the rate of change of image size. However, in order to use this source of visual information an important assumption must be made on the part of the viewer: all of the changes in the ball’s image size are due to the fact that it is getting closer. This assumption is a reasonable one to make as it is likely true 99.99% of the time.  But, notice I didn’t say 100%…

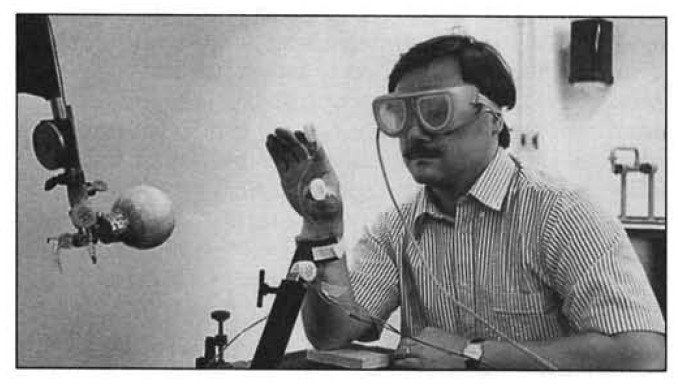
In one of my favorite experiments of all time, Savelsbergh, Whiting & Bootsma (1991) asked participants to try and catch balloons that were moved towards them as shown in the image below. The key manipulation in this study, was that for one of the conditions the balloon was deflated as it moved towards the observer.  Think about what this does to the retinal image. Because the balloon is getting closer to the observer its image size is increasing but at the same time the image size will decrease because it is getting physically smaller (due to the deflation).  The net result is the assumption is not met: the change in image size is not all due to the approach.

The basic findings of this study can be seen in the table below.  If we just compare the large and deflating ball, it is important to note that these two balls had the same actual TTC. That is, they arrived at the catcher’s hand at the same time. This should (but clearly doesn’t) lead to  similar hand movements for both.  Specifically, the time at which grasp is initiated is 10 msec later for the deflating ball.

When we look at the perceptual information this result makes complete sense. When a ball is deflated as it approaches an observer it will result in the rate of expansion of the ball’s image (dθ/dt in the equation above) being smaller than a comparable non-deflating ball.  This should make the catcher perceive the TTC to be longer (i.e., there is more time before the ball arrives) making them react later. Let’s now relate this to the football problem I started with.

Catching End Over End Passes and Kicks

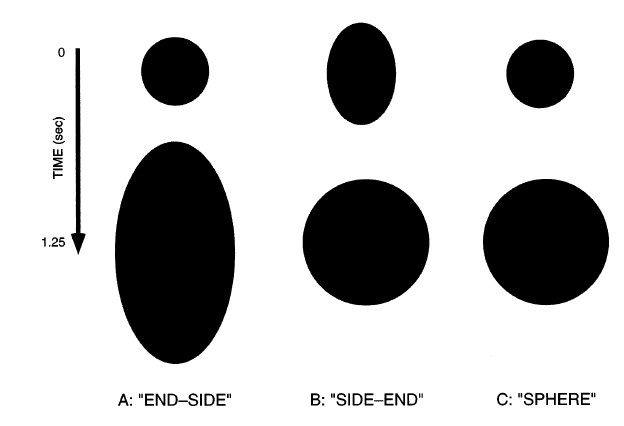
Another way in which the image expansion assumption can be violated is when the approaching object is nonspherical (like a football) and it rotates as it approaches the observer. Illustrated in the figure below are three different conditions that Martin Regan and I tested in a study published in 2000. A and B represent two cases of poorly thrown/kicked footballs: one in which the ball is first seen end-on then rotates 90 deg so that it is seen side-on just before the catch (“END-SIDE”) and one in which the ball is first seen side-on then rotates 90 deg so that it is seen end-on just before the catch (“SIDE-END).  The key point here is that the rotation of the ball is going to cause a change in the image size that is not due to the approach. Specifically, the vertical dimension of the “END-SIDE” ball will expand at a faster rate while the opposite will be true for “SIDE-END”. As shown in panel B below, for the “SIDE-END” condition, the size of the ball’s vertical dimension is actually the same at the beginning and end of its trajectory.

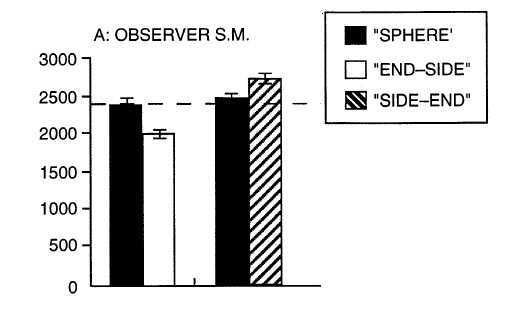
Using these stimuli, we performed an experiment in which observers had to judge the TTC.  Shown below are the results for one participant (similar results were obtained for all) when they were making estimates for balls with actual TTC values of 2400 msec. What can be seen here is that judgments are quite accurate for a rotating sphere, which was expected because rotation does not alter it’s retinal image. For the “END-SIDE” condition, the perceived TTC was roughly 400 msec sooner than the actual value. This again was expected because the rotation increases the rate of image expansion. Finally, as also expected, the perceived TTC for the “SIDE-END” ball was later than the actual value. Therefore, if a receiver or punt returner uses the optical variable tau to time their hand movements when catching they should close too late or too soon (depending on the rotation) making them drop the ball.

Summary

• Using the optical variable tau to catch an approaching ball requires that the rate of change of the ball’s retinal image is entirely due to it’s approach
• For slowly rotating balls this requirement is not met and may cause the receiver/returner to misperceive TTC and move their hands at the wrong time
• When we tested balls that rotated at higher rates (i.e. that completed several complete 360 deg rotations before reaching the observer) the estimation errors were eliminated suggesting that our visual system can filter out the image change due to rotation in such conditions
• Related to the point above, if a kicker is deliberately trying to create an end-over-end kick they should attempt to kick the ball so that it has a slow rotation rate

[/shadowbox]