[shadowbox]
The Psychology of Quick Pitching & Altering Deliveries
In recent years some prominent MLB pitchers have begun altering the timing of their delivery in an attempt to mess with batters (although it is not a new practice). A few examples of how Toronto Blue Jays pitcher Marcus Stroman does this can be seen in the excellent gifs created by Rob Friedman:
Marcus Stroman Messing with Trumbo’s Timing (Quick Pitch and Fake Quick Pitch). pic.twitter.com/rIq5CRz32x
— Rob Friedman (@PitchingNinja) June 28, 2017
Several different techniques can be seen here including borderline quick pitching (rushing the delivery to throw the ball before the batter is set), faking the start of a delivery, and pausing in the middle to add some body gyrations before releasing the ball. An even more extreme example of the latter (what Jeff Passan called “the rocking chair”) is used by now SF Giants pitcher Johnny Cueto:

This practice flies in the face of everything pitchers are traditionally taught: have a highly consistent and repeatable delivery. So why do they do it? How does altering a pitching delivery like this effect the batter?
Starting/Stopping Actions & The Horse Race Model
A baseball swing is a highly complex motor action that involves several different muscle groups (including the lower extremities, trunk, and upper extremity), has multiple phases of motor activation, and must be completed in a fraction of a second to be successful. For these reasons, a batter must initiate the action well before the ball is released. With most pitchers this is achieved by “timing the delivery”, that is using some cue from the kinematics of the pitcher (e.g, their foot leaving the ground or glove going up in the air) as a trigger to start the act of swinging. However, when the pitcher fakes their delivery or puts the hitter in the rocking chair the batter must inhibit this response or they will swing way too early.
The ability to suddenly stop a motor action has been investigated extensively using the stop-signal task (Slater-Hammel, 1960). This task is a variation of a simple reaction time (RT) measurement. On each trial the participant is presented with a go signal (e.g., a light turning on) and instructed to make a simple motor response (e.g., pressing a button) as quickly as possible when this go signal is detected. On some trials a stop signal (e.g., a brief auditory tone) is also presented and participants are instructed to inhibit the motor response when the stop signal is detected. In hitting, the “go” signal is the kinematic cue the batter uses to the time the pitcher during their normal delivery (e.g., Cueto’s front foot leaving the ground) while the “stop” signal would of course be his shoulder or leg shake during the rocking chair delivery.
One of the main findings of this line of research is that the probability of successfully inhibiting the motor response is inversely proportional to the stimulus onset asynchrony (SOA) between the go and stop signals (i.e. the time that elapses between them). This effect has been modeled as a “horse race” between independent stochastic processes responsible for producing and inhibiting the action (Logan, Cowan, & Davis, 1984). These two processes race toward a discrete point in the perceptual-motor processing stream (the point of no return) at which time there is a changeover from voluntary, continuous control of the action to involuntary, ballistic control. If the processing of the go signal reaches the point of no return before the processing of the stop signal the motor action will not be inhibited successfully. Because the processing times for these two signals are selected from random distributions, the success of inhibiting an action for a given SOA is probabilistic.
When we look at a more complex response than just pressing a button, there are actually different response outcomes that can occur in addition to stopping or not stopping the movement. By using an elbow extension response in a stop-signal task and measuring EMG activity from the arm, McGarry and Franks (2003) demonstrated that there can be two other outcomes: an interrupted response is defined as a movement that has the same initial EMG activity as a full response but then suddenly deviates from the full response profile after several milliseconds. A partial response is defined as a response that has EMG activity greater than baseline but has significantly lower activity than the full response. This suggests that in the race to the point of no return the “go” and “stop” processes are not completely independent and instead can interact to produce partial movements.
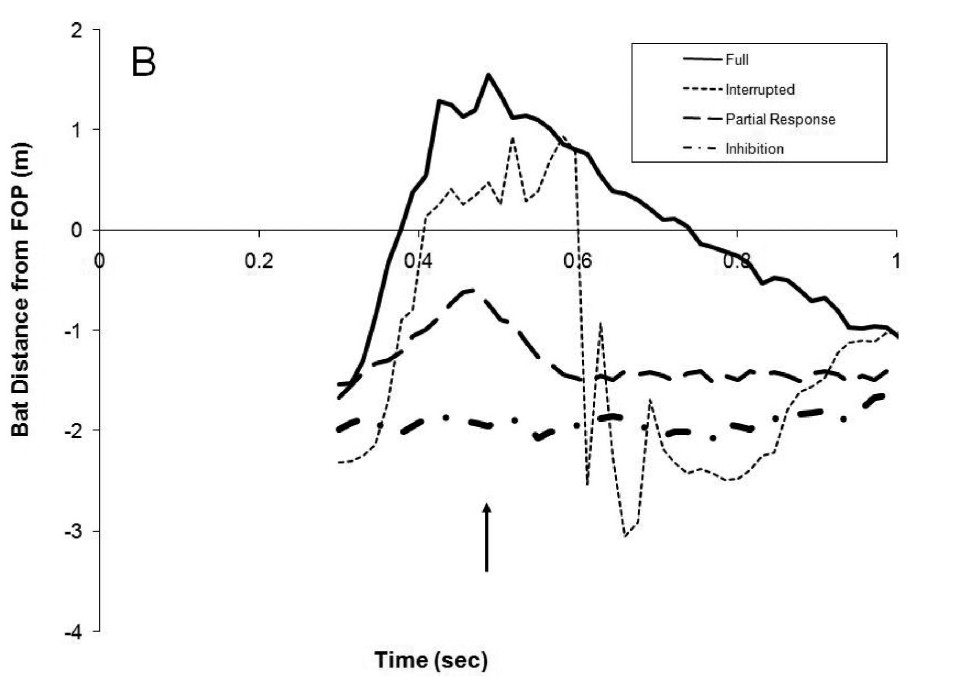
In 2009, I actually studied this in the context of baseball batting by looking at “check” swings. Using a modified version of the horse race model, I was able to show that whether or not a batter checks a swing successfully depends on at what point in the pitch trajectory the visual information about the ball’s actual trajectory deviates significantly from the expected trajectory (based on the count and pitcher tendencies). The figure below shows traces of bat movements for the 4 different outcomes I observed:
Figure 1 – The horizontal distance between the end of the bat and the front of the plate (FOP) is plotted as function of the time since the pitch was released. The arrow shows the instant in time when the ball crossed the front of the plate for this particular pitch speed and location.
When the actual trajectory matched the expected trajectory a full swing occurred (solid line) while when they were very different the batter fully inhibited the swing (thick dashed line). But for cases in between, there was essentially leakage in the control of the action — the batter moves their bat forward even though they don’t want to.
This has two important implications for altered pitch deliveries. First, it is likely that in many situations the batter will not be able to completely inhibit their muscle activity when they detect the “stop” signal in the altered delivery i.e., the “stop” horse won’t quite beat the “go” horse to the finish line 🙂 This leakage in activity will cause the batter to be slower to react when the pitch is delivered because they will essentially have to reset the movement during the delivery. Second, I would predict that an altered pitching delivery would be more disruptive when the alteration occurs later because it increases the SOA between the “go” and “stop” signals thus increasing the probability the “go” signal will get (at least partially) through. In terms of the examples I gave at the start of the post, faking a delivery should be less disruptive than pausing/gyrating at the top of the delivery.
A couple other practical implications before finishing this section. First, as I previously proposed, assessing a batter’s stop signal reaction time (SSRT) — that is, how quickly they can inhibit their swing in situations where it clearly should be — may be a valuable metric for assessing discipline and pitch recognition in batters. Estimates of SSRT have been used as a measure of self control in several different domains including aging, schizophrenia, and attention-deficit hyperactivity disorder. Second, it may be possible to actually improve SSRT through training, making a batter less susceptible to the effects of altered deliveries. A type of SSRT measure (which involves a binary response as opposed to a full swings) is currently being employed in the uHIT app by DeCervo.
The Effects of Unpredictability & Waiting on Reaction Time
The effects of varying the time between the start of a trial and the presentation of a stimulus (called the fore period) on reaction time (RT) has long been a topic of interest to researchers with studies going to back to the 1940’s. In this line of research two main effects are typically observed (reviewed Niemi & Näätänen, 1981). The most basic effect can be seen in the figure below. When the fore period is constant (i.e., the pitcher always has the same timing to their delivery) RT systematically increases the longer you make a person wait before responding:
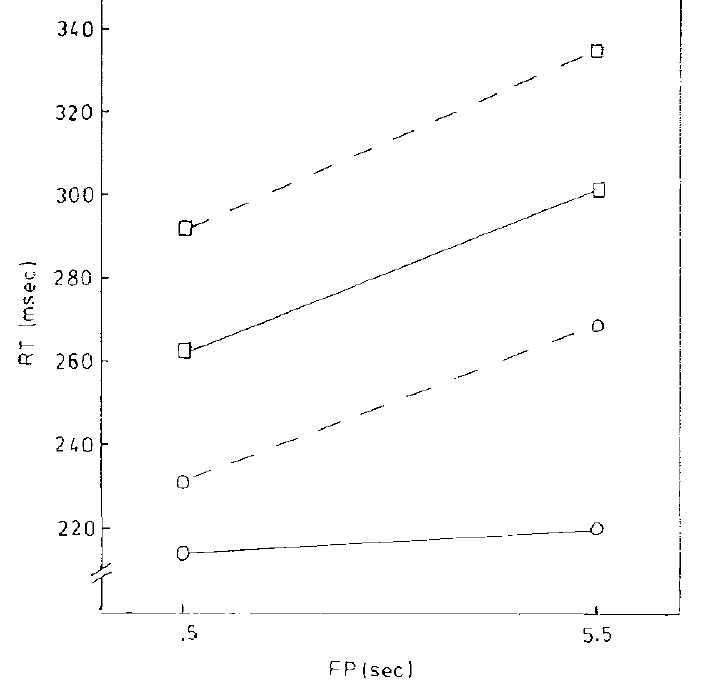
Figure 2 – RT as a function of fore period (FP)
The two exceptions to this rule are very short fore periods (< 300 ms) for which RT’s are slow and when the stimulus is a loud sound (flat line in the figure). It is has been proposed that this occurs for two reasons. When RT is constant, the observer can anticipate the required response by mentally timing the fore period. However, the accuracy with which we can estimate time intervals increases with their duration so anticipation would be more inaccurate with longer fore periods. Second, especially for more complex movements, motor readiness decreases with increasing wait time. It is for these reasons that “holding the ball” (i.e. waiting a long time before starting the delivery) is a frequent strategy used by pitchers.
The second effect commonly observed is that RT increases as the variability of the fore period increases:
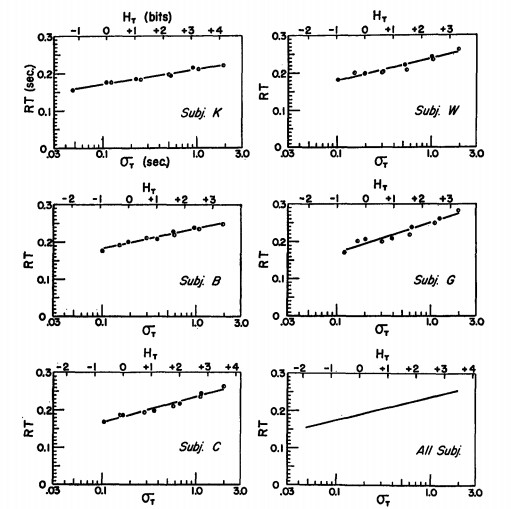
Figure 3 – RT as a function of the standard deviation of the fore period (from Klemmer, 1957)
As also shown in this figure, the effect of fore period variability can be quantified in terms of information theory. Specifically, increasing the standard deviation of the fore period increases the uncertainty which can be quantified in bits. From this data, it was estimated the RT increases 18 ms per bit of stimulus uncertainty. This is of course what is happening with altered pitching deliveries. When a pitcher uses a quick pitch or alters the timing of their delivery they are increasing the variability of the fore period and thus increasing the temporal uncertainty.
Summary
Alerting the timing of the delivery in pitching can make hitting more difficult because it can require response inhibition from the batter and can slow their reaction time to the pitch by increasing temporal uncertainty. On the pitcher’s side, for this to be most effective, the different timing techniques should be switched up frequently to increase fore period variability and pauses in deliveries should occur as late as possible to increase the likelihood of the “go” horse winning – resulting in movement leakage. On the batter’s side, the effect of altered deliveries can be counteracted through training to improve SSRT and practicing with variable fore periods.
[/shadowbox]