Recommended: Listen to the Podcast Episode that accompanies this analysis

Goal: To test the following two hypotheses: (i) a pitcher can overcome having a lower fastball velocity by being more unpredictable in the type of pitches they throw (i.e., high entropy) and (ii) pitching success will be significantly related to entropy

Data sources:
http://www.baseball-reference.com/play-index
http://www.brooksbaseball.net/

Inclusion criteria: Pitched 162 innings or more in the 2015 MLB Season

Data removal: R.A. Dickey was removed as an outlier, Entropy (0.3 bits) more than 6 standard deviations below next lowest player

Formulae:
For a pitcher that throws a fastball (FB), curveball (CB), slider (SL) and chaneup (CU):
Entropy = -(pFB*lnpFB + pCB*lnpCB + pSL*lnpSL + pCU*lnpCU
wherepFB =proportion of fastballs, pCB=proportion of curveballs, etc

Standardized Entropy = Entropy/ln(Number of Pitch Types)

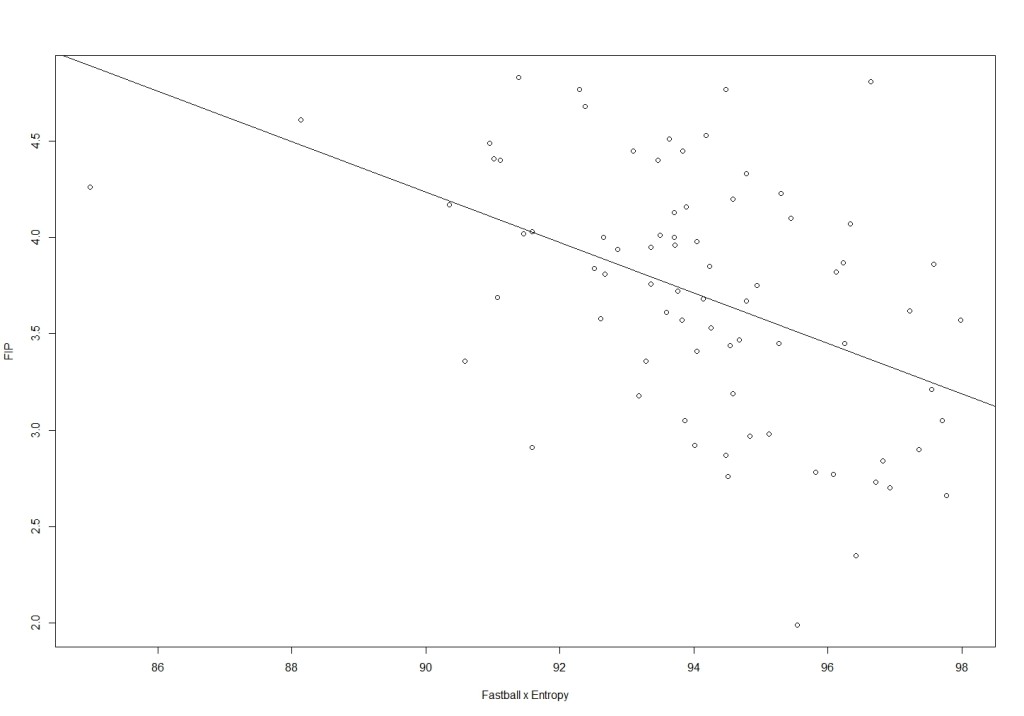
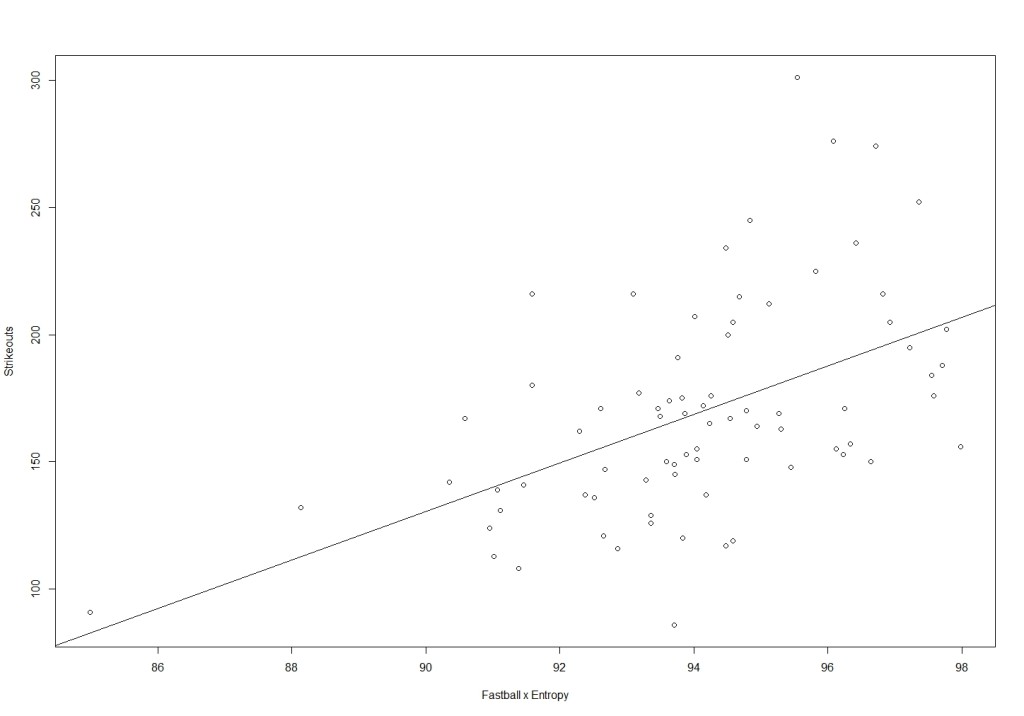
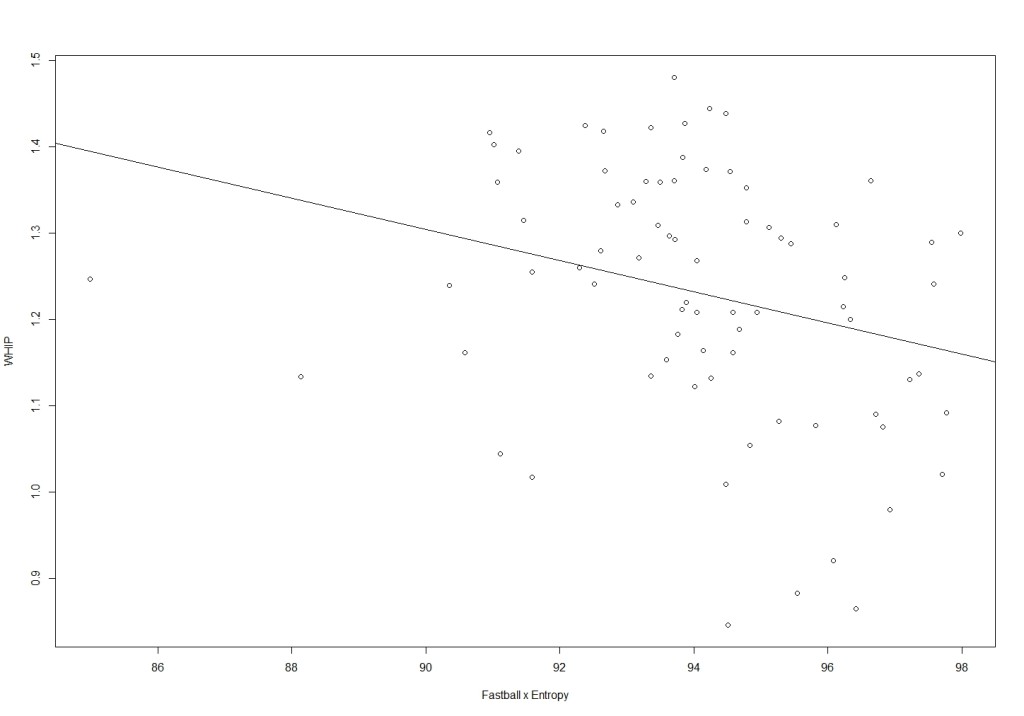
Fastball x Entropy = FastballV +(Standardized EntropyN – Standardized EntropyAVG)

Results:
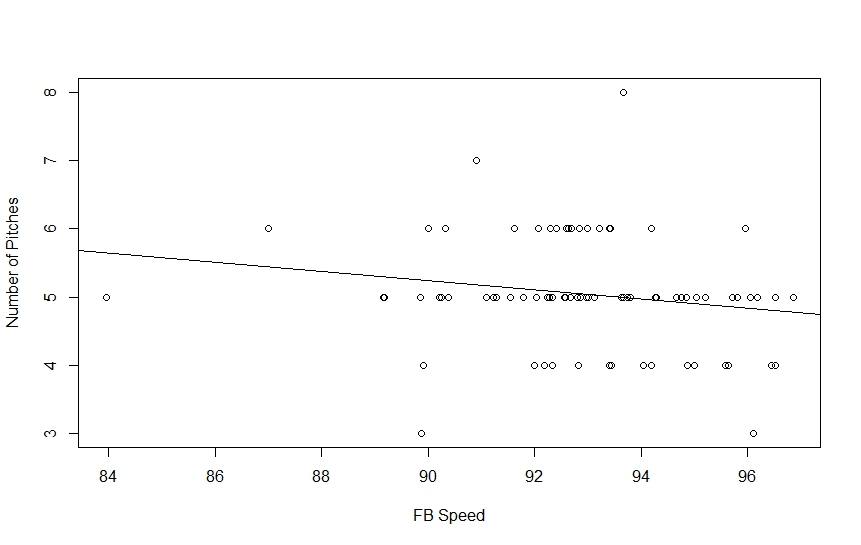
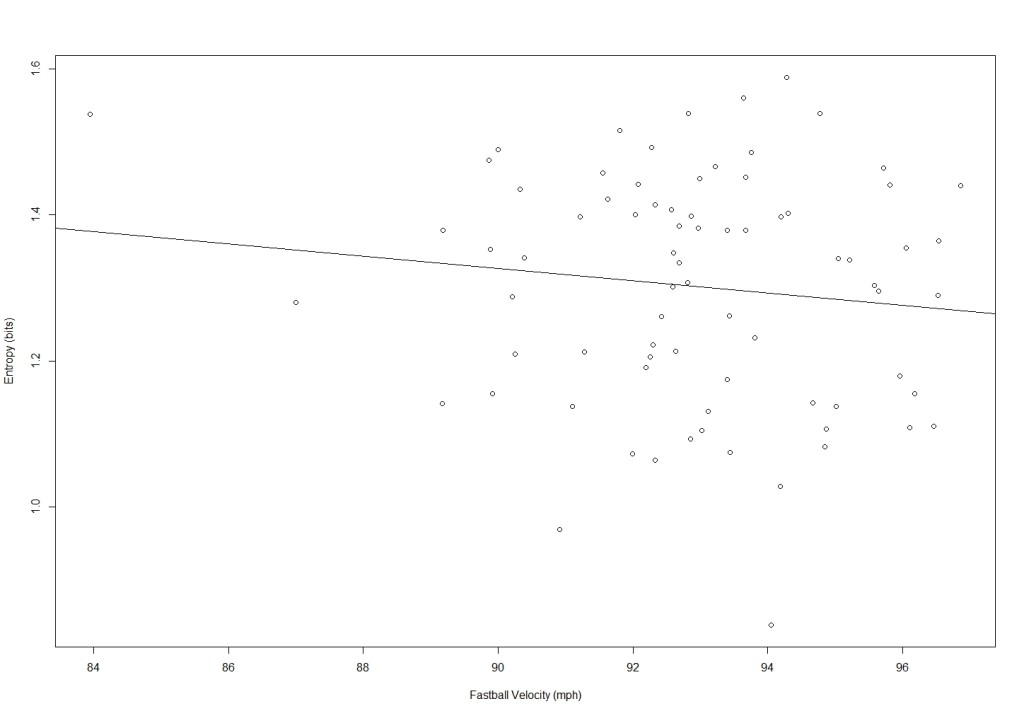
1)Entropy vs Fastball velocity

2)Pitching Performance vs Fastball x Entropy
Fielding Independent Pitching (FIP)

Strikeouts (S)

Walks + Hits /Innings Pitched (WHIP)