[shadowbox]

A Baseball Batter’s Perception of Spin & How it Relates to Hitting Performance

One of the most interesting measurements that has come from the “Pitch f/x – Statcast Era” in baseball is pitch spin rate.  While there has been a lot of discussion of how spin influences the flight of the ball, how it varies within and between pitchers, and how it relates to outcomes at the plate, I haven’t seen much discussion about how spin is perceived by a batter. Can a batter actually discriminate spin rate visually? Is there a perceptual RPM limit? Why do pitches with above or below average spin rates tend to give a batter troubles? Do batters use an internal model of gravity when judging pitch trajectory? Is there a way a batter can counteract the effects of spin through training? Let’s explore…

Some Basics about the Physics of Spin

For my purposes, I want to just consider the most basic case of spin: a four-seam fastball. For the typical four-seamer (shown below) there is pure backspin on the ball so that the axis of spin is perpendicular to the direction the ball is travelling.[/shadowbox]

Video source: https://www.kchitter.com/baseball-rotation/

[shadowbox]

This type of spin, known as useful spin, has a direct effect on the flight of the ball. Specifically, the spin creates air turbulence behind the ball resulting in Magnus Force which pushes the ball upwards and counteracts gravity. This produces the basic relationship: the higher the spin rate on a four-seam fastball the less it will drop in height as it travels from the pitcher’s hand to the plate. The effect is not huge…we are talking a matter of  a few inches for large ranges of spin rate.  But it doesn’t take much difference to change a hit from solid to weak contact.  For example, for an 87 mph four seam fastball, a backspin rotation rate of 2400 rpm will result in a pitch that crosses the plate 2.75″ higher than the same pitch thrown with a 1800 rpm rotation rate. For reference, the width of a typical baseball bat at the “sweet spot” is roughly 2.5″.

The excellent GIF from Driveline Baseball shows the difference in path of travel for balls of different spin rates:

Spin Rate & Batting Performance

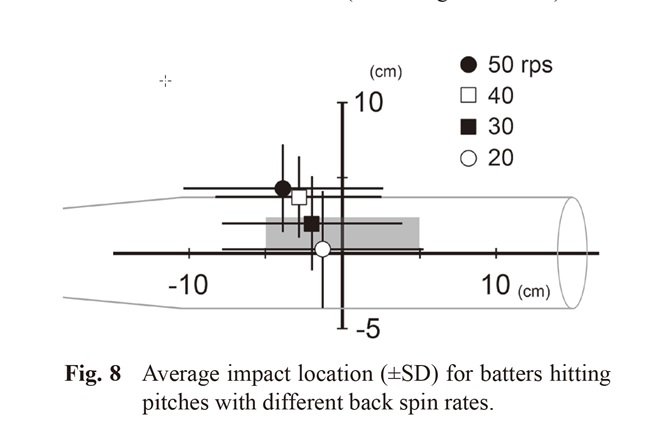
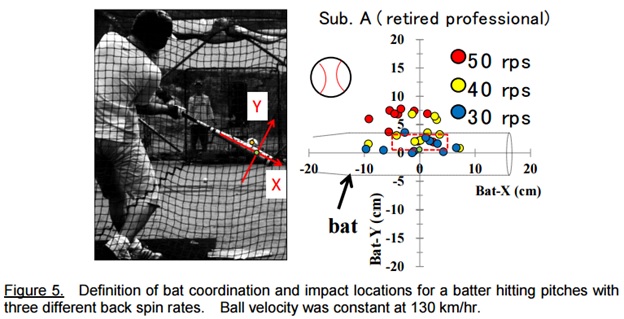
On a surface level, the effects of spin on batting performance are what we might expect based on the on the ball flight. In controlled experiments, it has been shown that as spin rate is increased above the “typical” rate for a particular velocity batters swing more under the ball while if it is decreased they swing more over it. This can be seen in the data from Highuchi et al. (2013), see also the paper by Kanouse et al .

In this experiment, the pitch velocity was 80.5 mph which is typically (based on league averages) associated with a spin rate of 30 rps (1800 rpm). Note that batting performance was the best (i.e., contact closest to the sweet spot of the bat) when this typical rate was used. For higher spin rates, the point of contact was higher up on the bat (which would produce a pop-up if high enough) or the ball was missed completely. For the pitch with the lower spin rate (20 rps, 1200 rpm) the contact point was lower down on the bat (which would produce a ground ball if low enough). Analysis of data from MLB has provided some agreement with the results of this study as it has been shown that for a fastball of a given velocity the % of swings and misses goes up as spin rate increases however the relationship between swing outcomes and spin rate is much more variable in these data.

OK, now that we are done with the preliminaries, let’s dig a bit deeper into the batter’s perception of spin..

What Perceptual Information is used to Judge Spin Rate?

What determines how fast we perceive an object to be spinning or rotating? The answer is more complicated than you might think because when an objects spins it contains both angular and linear motion components.  This can be best understood by thinking about a windmill:

In angular motion terms, this windmill completes one 360 deg revolution in about 4 sec, so it has a rotation rate of 0.25 rps.  But now let’s focus on the movements of specific parts of the windmill, for example the very tip of one of the blades. Over a very short time interval, the tip will be moving in a straight line thus we can calculate an instantaneous linear velocity for it.  Now let’s compare this linear velocity for the tip of the blade and the thick part of the blade near the windmill’s center.  For each revolution, the tip of the blade travels a much larger distance than the spot near the center and, thus, has a higher instantaneous linear velocity.  So, for a spinning object with a given angular velocity there is an associated set of linear velocities. Why am I bringing this all up? Because, research has consistently shown that the perceived spin rate of a rotating object depends on a combination of both the angular and linear velocities.  This can mostly easily be demonstrated by changing the size of a rotating object. For example, if I doubled the length of the blades of the windmill shown above it would double the linear velocity of the tip of the blade because it would now be further from the blade’s center. But the windmill would still complete one revolution in 4 sec so its angular velocity would be the same. What happens in this situation? Observers perceive the spin rate as being higher when the size of the object is increased.

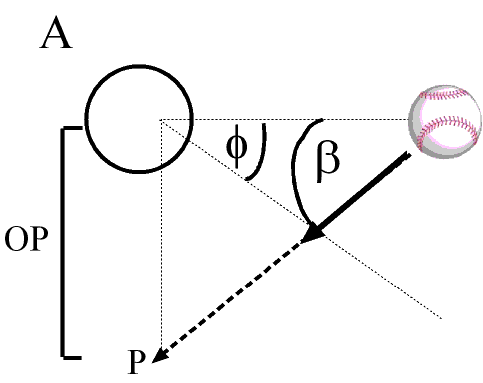
All of this is relevant to baseball because, just like with the arms of the windmill, the different parts of the laces on a ball have linear velocities that will influence the batter’s perception of spin. And this is a problem. Imagine that I picked up the windmill I have been talking about and just dropped it while it was spinning.  In this situation, the instantaneous linear velocity of the laces will be influenced both by the spin rate and the drop rate. So, in other words, changes in ball trajectory will likely contaminate the perceptual information used to judge spin rate because they will add linear motion.  Martin Regan and I actually found an effect that supports this idea in a study we conducted in 2006.  In the experiment, experienced baseball players were presented with simulated rotating baseballs (with laces).  The first ball they saw always had the same spin rate, while the spin rate of the second ball varied. We always systematically varied the speed and direction of motion in depth of the second ball to determine whether these influenced the perception of spin rate.  The participant’s task was to indicate which ball was spinning faster. We found that the the experienced baseball players could not judge the spin rate independently of the direction. Specifically, when the trajectory angle β (shown in figure below) was larger, the ball was perceived to be spinning at a higher rate. This effect is what was expected because increasing β resulted in higher linear velocity of the laces.

Another potential problem associated with judging the spin rate of a baseball pitch is aliasing. A common example of aliasing I think many people may have experienced is in a video in which a computer monitor is being filmed.  Sometimes when this is done you can get this:

What’s happening here is the frame rate of the camera is too low to effectively sample the refresh rate of the computer monitor.  So we end up seeing the trace lines. According to Nyquist’s Theorem we need to sample at twice the rate of the signal we are trying to capture.

OK, let’s apply this to baseball. Imagine that I have a pitch that has a spin rate of 50 rps and I film it with a camera recording at 50 frames/sec. Further imagine that I perfectly synchronize the start of the spin and the start of the filming.  What spin would I see? Absolutely none. Think about it..when the pitch is released the part of the laces marked with the ‘X’ in the figure below would be on top of the ball.

With a spin rate of 50 rps the the ‘X’ would be in the exact same spot 20 ms later because the ball made one full revolution in that time. So, the ‘X’ would be at the top at time points 0, 20, 40, 60, 80, etc..A camera operating at 50 frames/sec essentially takes a static photograph every 20 ms and pieces them together. So, in this example, every frame would just show the ‘X’ at the top and the ball would look like it was not spinning at all. The frame rate of the camera is too slow to faithfully recreate the signal (the spinning ball). According to Nyquist, we would need a camera that recorded at ≥ 100 frames/sec to do this. What would happen if the frame rate was somewhere between these two values, say 60 frames/sec?  We would see the ball spinning but at different rate than the real spin. If you get just the right combination of sampling and signal rate you can even get the rotation direction to change in the so-called “wagon wheel illusion“.

So, would the human eye suffer from the same aliasing problem?  Possibly, yes. Its actually hard to get a consistent estimate of the sampling rate of the human eye. I have seen it quoted anywhere from 30 Hz (i.e., samples/sec) to over 60.  But with pitch rates up to 50 rps we would need at least at sampling rate of 100 Hz.  So I think it is likely that for at least some pitches our eye will not sample at a high enough rate to faithfully capture the spin rate.

OK, given the contamination by linear velocity and this potential aliasing problem it doesn’t sound like hitters would be very good at detecting pitches with different spin rates. But what does the data tell us…

How Good are we at Judging the “Spin” of a Pitch?

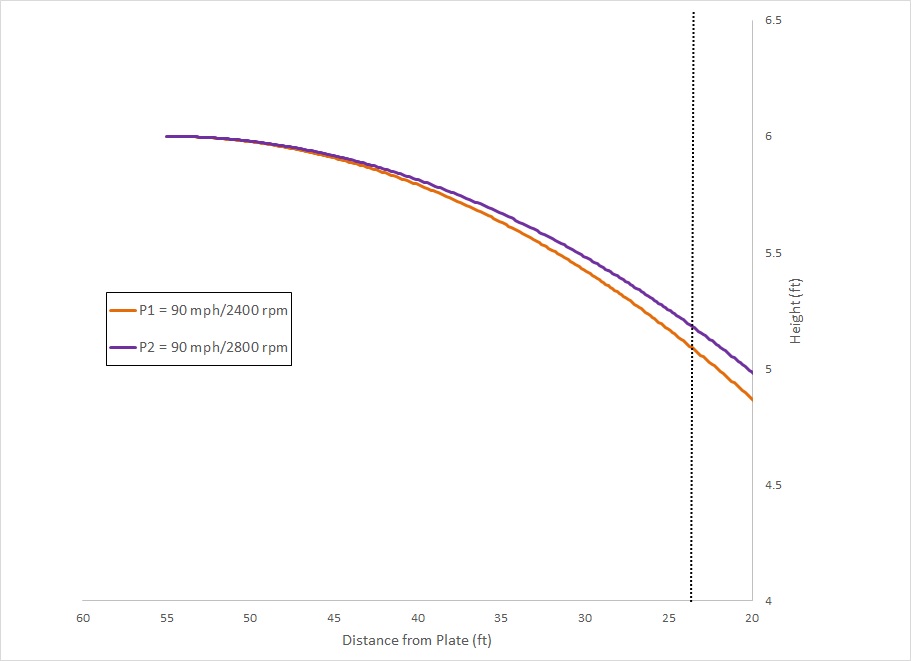
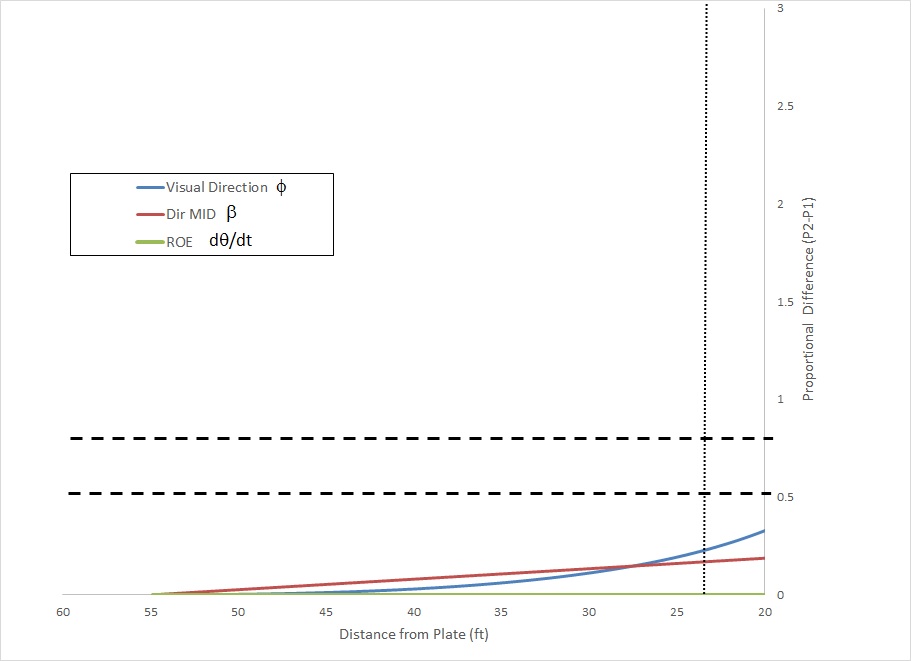
First off, it is important to note that two pitches that have the same velocity but (even a very large) difference in spin rate meet my definition of “tunneled pitches” which I discussed in my previous blog post.  For example, if we compare two 90 mph pitches, one with the league average 2400 rpm for that velocity and one with the highest fastball spin rate recorded in MLB of 2800 rpm we get:

Figure 1

Figure 2

From Figure 2 it is clear that the perceptual information that could be used by the batter to discriminate the time to contact, visual direction and direction of motion in depth of these pitches are all well below threshold up until the swing decision point 23.8 feet from the plate (see my pitch tunneling post for descriptions of these information sources).  In other words, even for a large difference in spin rate the batter could not tell the difference between the two pitches based on their trajectory. So, let’s turn to perception of spin…

How good are we at discriminating different rates and direction of spin? In the 2006 experiment I mentioned above in which experienced players had to judge which of two pitches was spinning faster we measured discrimination thresholds.  In our study, the rotation rate varied from 450-750 rpm (so obviously much slower than real pitches).  What did we find?  Weber fractions (see here for definition) for spin rate discrimination ranged from 0.2-0.3 for the different participants.  If we apply this value to a MLB average spin rate of 2400 rpm (which is exactly what calculating Weber fractions allows us to do!) then this means batters would require a difference in spin rate between pitches of at least 480-720 rpm to be able to reliably tell which one is spinning faster. So for the two pitches shown in Figure 1 above (i.e., 2400 vs 2800 rpm) the perceptual information for perceiving the rate of rotation would also be below threshold for most batters.  In 2015, Shapiro and colleagues found similar results, in this case for judgments of rotation direction. They used a real baseball mounted on a spinning driveshaft. While, observers could easily judge the direction for spin rates up to 1200 rpm, as the spin rate went above 2000 rpm their performance in judging direction was at chance level.

Finally, the subjective impressions of batters seem to be pretty consistent with this inability to pick up spin rate information. Instead of talking about different spin rates, batters often refer to crude features that can be seen as the ball approaches as this infographic from Coach Matt Lisle nicely illustrates:

What the batter sees. pic.twitter.com/EFGqRq8mlf

— Matt Lisle (@CoachLisle) March 27, 2015

How and Why Does Spin Rate Affect Batting Performance?

For me, this is the most interesting question of all because I don’t think we have looked at the common answer given carefully enough. To review, the basic story is: batters swing under fastballs (resulting in misses or pop-ups) with abnormally high spin because the Magnus force holds the pitch up more, while they swing over fastballs (resulting in ground balls) with abnormally low spin rate because the force holds these pitches up less.  Sounds straight forward enough. But more or less than what?  The average MLB fastball?  That is a concept available to statisticians not hitters. For a batter to be fooled by a pitch with a low or high spin rate they must have been expecting the ball to drop at some other rate. What is this expectation and where does it come from?

Several studies have shown that we have a built-in, internal model of the effects of gravity on a projectile.  For example, as shown by McIntyre and colleagues, if we try to catch or punch a ball dropped from above the timing of our movements are well synchronized to the ball’s arrival when it accelerates by the normal gravitational force of 1g. Movements made towards a ball moving under 0g conditions (in computer simulations or experiments conducted in Space) are always timed too early and even with extensive training we don’t seem to be able to correct this.

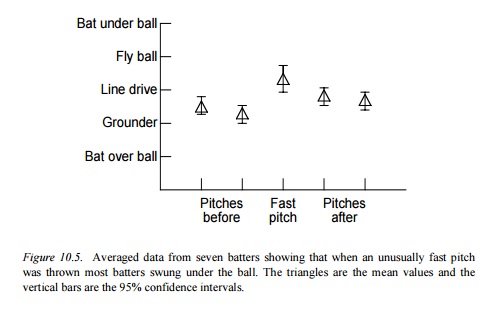
Therefore, when a batter steps to the plate I think it is reasonable to assume that they have an a priori prediction about the most likely path of the ball that is based on some internal model which incorporates the effects of gravity.  This prediction can then of course be updated with perceptual information once the ball is released. (But as I have said, the perceptual information related to spin rate is very weak!).  Thus, since differences in spin rate are pretty much undetectable to a batter, when a pitch is thrown with a spin rate that is not consistent with their internal model they will make a prediction error. Supporting evidence for this predicted path idea can be seen by the fact that the effects of having a pitch with an abnormally high spin rate are similar to those produced by introducing an unexpectedly fast pitch. As can be seen in the data from Bahill & Karnavas (1993), when a fast pitch is introduced (which would drop less as it approached the plate than the hitter was predicting) batters tend to swing under the ball and hit more flyballs just as they do for pitches with a unexpectedly high spin rate.

How this internal model is aligned with spin rate is open to question. For example, is a batter’s internal model calibrated for the spin rate they see most often (which would then presumably align with the MLB average rate)? Can they recalibrate this internal model for the spin rate of specific pitchers if they face them enough? From the 0g research I described above, it seems like this might be difficult. But maybe it could be helped by introducing pitches with variable spin rates in practice? I hope to explore these ideas more in future posts..

Take Home Messages:

• Spin rate can alter the flight of ball by making it fall more or less than is typical for a given velocity
• The perceptual information for detecting differences in spin rate is quite poor and experiments have shown that very large differences are required to discriminate rate and direction of spin
• It is proposed that spin rate influences batting performance because batters have an internal model of how a pitch falls due to gravity which assumes some fixed value of spin rate. This model is used to generate a prediction about the most likely path of the ball.
• Whether a batter can recalibrate their internal model by practicing under different spin rate conditions is something that should be explored

[/shadowbox]